Hash设计原理(上)
理解HashMap底层,首先应该理解Hash函数,今天我们聊聊什么是Hash函数以及Hash函数的设计、
查找速度的困扰
算法国自建立起,就以快速为至高的荣誉,O(n^2) 时间复杂度的设计常常被人嫌弃,一般都想着弄个O(logn)
算法国最近遇到了一个问题,就是随着处理数据的逐步增大,查找的时间越来越大了
之前用的数组和链表,最后改成二叉查找树,可是这些都需要和其中的元素进行比较,比较的次数越多,查询的速度就越慢
国王想着能不能有一种办法,查找某个元素的时候,不需要比较,直接就得到这个元素,时间复杂度直接就为O(1),和集合中的元素个数就没有关系了
初次的方案
国王召集各大臣讨论此事
“如果不需要比较,我们可以借鉴数组下标访问的思路来做”,经验老道的王大臣发话了
“哦,怎么个设计?”何大臣问道
“你看,我们要访问数组中某个元素怎么访问?”
“只需要知道起始位置和下标值就可以了,不管数组中有多少个元素,都可以一次访问到,这正是因为起始位置和下标值组成了元素的存储位置,从这个存储位置就可以直接找到元素”,王大臣自问自答起来
左丞相接着道,“所以说,给定一个元素,我们只要得到该元素的位置,也就是说将元素和元素位置建立一种一一对应的关系,就可以迅速定位要查的元素了”,说着说着,王大臣在纸上画起了图
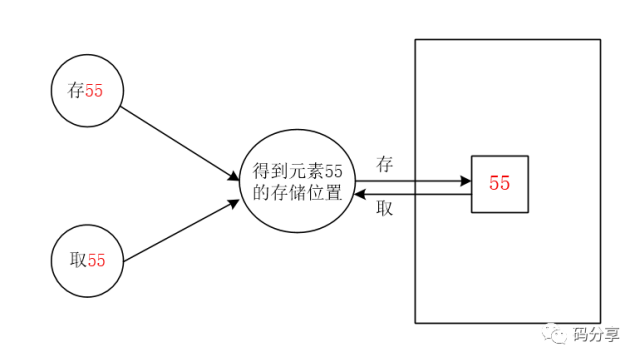
“现在问题的关键就是输入55,我们如何知道元素55的存储位置”,何大臣说道
“对”,王大臣答到
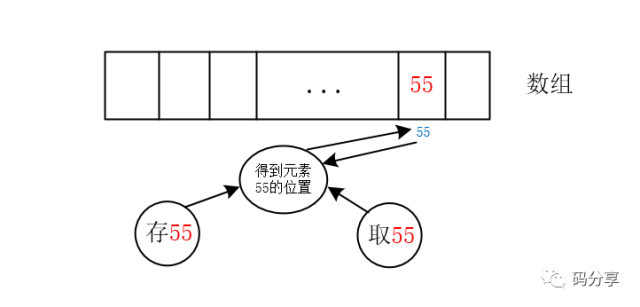
“如果输入的数为正整数的话,我们完全可以用数组存储,用这个输入的正整数作为数组的下标来存取元素”,王大臣说道
“比如说55,我们就存到下标为55的位置,这样是不是很简单”,王大臣举了一个例子,顺便画了一个图
Hash函数的出现
“这也太理想了吧,现实生活中要存储的元素(key)的取值范围一般很大,比如说正整数,不可能为无穷多个正整数分配无穷大的数组吧,这不现实
就算有无穷大的数组,但实际存储的元素的范围可能很小,比如输入大多数在1-100之间,只有极少数的是其他数,那预先分配的那些空间不是浪费了吗?”,何大臣立马驳回了王大臣的想法
“那依你看,如何是好?”王大臣问道
“我看,既然输入的元素的范围可能很大甚至无穷,而我们的内存有限,所以说我们需要一种函数映射关系,将这些无限的元素映射到我们有限的内存地址上”,说着说着画了一个图
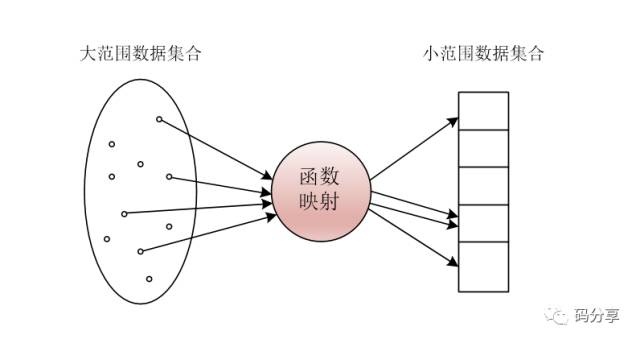
“很显然,多个数据有可能被映射到同一个地址上,我们暂且称为冲突吧”,何大臣说道
“我们给这个函数映射起一个名字,就叫Hash函数吧,这个Hash函数代表着一类函数,即把任意范围的元素可以通过映射关系压缩成固定范围的元素”何大臣说道,大家一致同意
Hash函数的选择
“那现在的问题就很清晰了,一个是这个Hash函数该选择什么样具体的函数,另一个就是出现冲突该怎么办?”王大臣说道
“如果是正整数,我们可以用这个正整数数除以某个数,取其余数,即我们常用的 k % m,k为正整数,m 为除数
这样一来,范围就缩小了很多,比如说 15%10=5,26%10=6,…,所有的正整数经过运算,都变成了 0-9 范围之间的数了,这样范围就缩小了很多”何大臣发挥了他数学的才能
大家一致称赞
m 的选择
“如果是这种做法,m 的选择就非常重要了,如果 k 值分布均匀还无所谓,如果 k 值具有某些特征
比如说 k 的个位基本上不变,而高位分布均匀,如 15,25,45,65,85,95,155,这么一组数据,经过你刚才的 k%10不就全部落在5这个位置上了吗?”一直没有说话的另一个李大臣发话了
这个李大臣虽少言寡语,但非常有才能
“对对对”,何大臣连声说道
“我们必须要使得经过Hash函数后关键字的分布均匀,尽量减少冲突,所以针对不同类型的关键字要有自己特定的Hash函数,整数应该有整数的Hash函数,字符串应该有字符串的Hash函数
就算针对同一类型的关键字,如果它具有某种规律,我们也要具体情况具体设计,刚才李大臣说的那种情况,我们就得选取其他分布均匀的高位来进行Hash”右丞相补充道
“那为何不优化一下我们的Hash函数来使得关键字分布均匀,比如说 m 取一个素数,这样就不会出现刚才的情况了,比如说m取11,15,25,45,65,85,95,155,这些数Hash后就会变成这个”,李大臣说着说着画了一个表

“这样就分布均匀,冲突很少,所以我们只需要用一个长度为11的数组来存储就行,只比你原先的10多了一个长度”李大臣补充道
“如果事先知道元素的分布情况,那我们可以针对特定的元素来设计Hash函数,如果不知道的话,那我们就提前想一个比较好的Hash函数,来应对各种可能出现的情况
不管怎样,我们最终的目的就是让各个关键字均匀的Hash到不同的位置”,国王看天色渐晚,总结了一下,然后说道,今天就到这里,明天再议
