别再问我什么是时间复杂度了
时间复杂度是学习算法的基石,今天我们来聊聊为什么要引入时间复杂度,什么是时间复杂度以及如何去算一个算法的时间复杂度
一、刻画算法的运行时间
某日,慧能叫来了一尘打算给他补习补习一下基础知识,只见克写了一段非常简单的代码








一尘看老师有点生气,开始虚心请教了



为了方便讨论,这里我们把每一条语句的执行时间都看做是一样的,记为一个时间单元



① 蓝色框的两条语句,花费两个时间单元
②黑色框的一条语句,花费n+1个时间单元
③红色框的两条语句,花费2*n个时间单元

这不是数学吗,一尘心里想到

其中的n被我们称为问题的规模,其实就是你处理问题的大小
慧能顺手画了这个函数的图
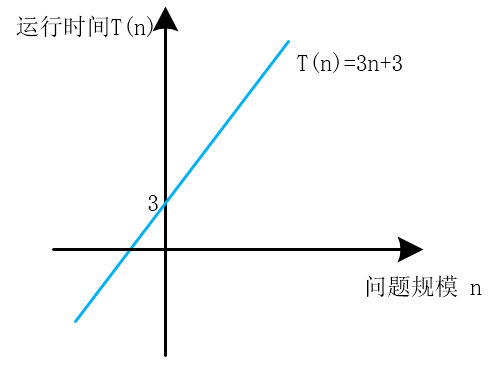
本文主要讨论问题规模和运行时间的关系,假定不同输入和运行时间基本无关





二、时间复杂度

比如说:T(n)=3n+3, 当n非常大的时候常数3和n的系数3对函数结果的影响就很小了
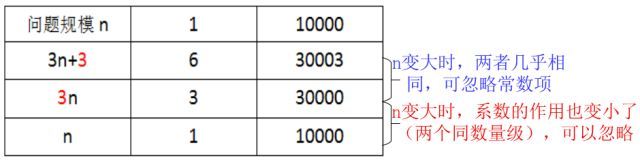

比如:
T(n)=n+1 忽略常数项 T(n)~n
T(n)=n+n^2 忽略低阶项 T(n)~n^2
T(n)=3n 忽略最高阶的系数 T(n)~n




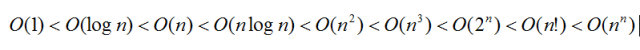
还好不用掌握那头疼的数学,一尘心中想到

一尘把话题又拉了回来



更准确地说O代表了运行时间函数的一个渐进上界,即T(n)在数量级上小于等于f(n)

三、时间复杂度的计算

一、得出运行时间的函数 二、对函数进行简化
①用常数1来取代运行时间中所有加法常数
②修改后的函数中,只保留最高阶项 ③如果最高阶项存在且不是1,则忽略这个项的系数



O(1)也被称为常数阶





一尘随手写了一段嵌套循环的代码




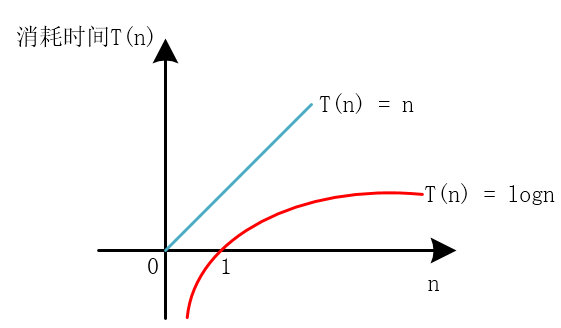
接着,慧能又写了一段时间复杂度为对数的代码
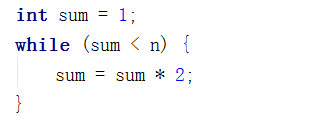


一向数学不太好的一尘此时有点懵








评论(9)
图挂了
手机不知道为啥,加载我的 gitee 图片出现了一些问题,你电脑看看勒
图片无法查看,什么原因?很多都是这样
不会啊,我在手机和电脑打开这篇文章都没事哦
老师,我还要
写得通俗易懂,感谢
原来如此,冲冲冲!
原来可以这么简单
很赞!