递归训练四：Leetcode 4. 寻找两个正序数组的中位数
题目描述
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
示例 1：
输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2
示例 2：
输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5
示例 3：
输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000
示例 4：
输入：nums1 = [], nums2 = [1]
输出：1.00000
示例 5：
输入：nums1 = [2], nums2 = []
输出：2.00000
提示：
- nums1.length m
- nums2.length n
- 0 <= m <= 1000
- 0 <= n <= 1000
- 1 <= m + n <= 2000
- -106 <= nums1[i], nums2[i] <= 106
原题链接：https://leetcode-cn.com/problems/median-of-two-sorted-arrays/
题解
这道题有一定难度，如果两个数组的长度和为奇数的话，那么这道题简单一些；但如果两个数组的长度和为偶数时，这道题的难度顿时上升了
为什么呢?因为你要求出两个数，然后再来求平均，而且主要，这两个数可能一个数是位于 arr1 数组，而一个数是位于 arr2 数组，这会导致我们的判断逻辑变的很复杂，不信的话，你可以去试试。
当然，如果你用一个临时数组把两个数组合并起来，然后求它的中位数，这肯定简单，不过我们要的是时间复杂度为
O(log (m+n))算法，下面开始讲解。
那怎么办呢？实际上，这道题我们是可以进行一下转换，就是无论两个数组的长度和是奇数还是偶数，我们都求出第 （m+n+1)/2 小数以及第 （m+n+2)/2小数，然后求这两个数的平均数，就可以了。这样，我们就屏蔽了奇偶数的影响，会容易一点。
所以现在的问题转化为如何求两个有序数组的第 K 小数，这个也有一定难度，但比上面好多了。
下面我随便讲一下如何用递归来求：我们可以采用递归的方法不断缩小 K 的，把求第 K 小元素转化为第 (K-K/2) 小元素….我举个例子吧，比较容易理解。
我们假定 arr1 = [1, 2,3]，arr2 = [3,4,5,6]，K = 4。
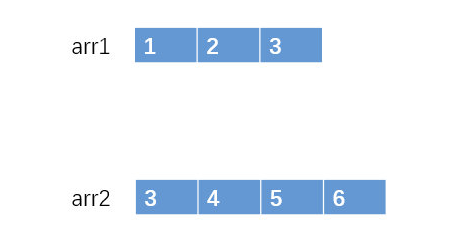
这里令 K = K- 1(说明：这里我们假设K从 0 算起，也就是有第 0 小元素，相当于令 K = K – 1)
如果不懂，你就先跟着我的思路走，之后再来想
再令
mid1 = K/2 = 1。
mid2 = K/2 = 1。
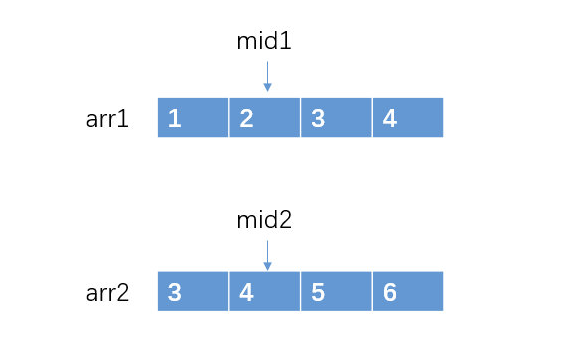
假如 arr2[mid2] > arr2[mid1]，那么我们要找的目标数是一定存在于 arr1[mid1+1…m] 和 arr2[0…mid2]中。而不可能存在于 arr1[0…mid1] 和 arr2[mid2+1…n] 之中。
那么问题转化为在数组 arr1[mid1+1…m]和数组 arr2[0…mid2] 寻找第（K-md1-1）小的元素，然后不断重复这个过程，直到 k < 1 或者 数组的左边界大于右边界（就是二分查找中的 left > right，那么递归就要结束了）
不过这里需要注意的是，有可能 k/2 的值是大于 m 或者 n 的，所以如果 k/2 > m 或者 n 的话，我们直接令 mid1 = m-1 或者 mid2 = n-1 就行了。
所以这道题的代码如下，下面有详细注释
class Solution {
// 由于中位数会受长度是奇偶数的影响，所以我们可以把问题转化为求
// 第（m+n+1)/2 小数以及第 （m+n+2)/2小数，然后求这两个数的平均数
public double findMedianSortedArrays(int[] arr1, int[] arr2) {
int n = arr1.length;
int m = arr2.length;
// 注意是除以 2.0，因为结果有可能是小数
return (findKth(arr1, arr2,(n+m+1)/2) + findKth(arr1,arr2,(n+m+2)/2))/2.0;
}
// 求第 K 小的数，这是一个辅助函数
public int findKth(int[] arr1, int[] arr2, int k) {
if(arr1 == null || arr1.length < 1)
return arr2[k-1];
if(arr2 == null || arr2.length < 1)
return arr1[k-1];
// 注意这个函数的参数有7个，上面那个函数的参数只有3个，同名不同函数哈
return findKth(arr1, 0, arr1.length - 1, arr2, 0, arr2.length - 1, k);
}
//参数 l1 和 r1 表示我们只截取了数组 arr1[l1...r1]这一部分元素，l2 和 r2 同
public int findKth(int[] arr1, int l1, int r1, int[] arr2, int l2, int r2, int k) {
// 递归结束条件
// l1 > r1，那么目标元素只可能在 arr2 中
if(l1 > r1)
return arr2[l2 + k - 1];
if(l2 > r2)
return arr1[l1 + k - 1];
if (k <= 1)// 注意，k == 0的结束条件与上面两个结束条件不能颠倒。
// 如果 k = 1，那么
return Math.min(arr1[l1],arr2[l2]);
int md1 = l1 + k/2 - 1 <= r1 ? l1 + k/2 - 1: r1;
int md2 = l2 + k/2 - 1 <= r2 ? l2 + k/2 - 1: r2;
if(arr1[md1] < arr2[md2])
return findKth(arr1, md1 + 1, r1, arr2, l2, r2, k - (md1-l1+1));
else
return findKth(arr1, l1, r1, arr2, md2 + 1, r2, k - (md2-l2+1));
}
}
对于这道题，还是挺难的，特别容易出错，如果你是新手，看不懂，那么可以先放着，后面在来看。